Floating Point Unit

---

ST-Floating Point Unit

Some STM32 microcontrollers have an internal FPU (Floating-Point Unit) that can accelerate floating-point arithmetic operations by executing them in hardware instead of software emulation for these operations which takes a bit longer time compared to the hardware FPU performance.

ARM Cortex-M cores support a hardware FPU with only single-precision (SP), double-precision (DP), or no FPU at all.

• Single Precision: M4, M33, M35P, M55
• Double Precision: M7
• No FPU: M0, M0+, M1, M23, M3

Overview

The various types of floating-point implementations over the years led the IEEE to standardize the following elements:

• number formats
• arithmetic operations
• number conversions
• special values coding
• four rounding modes
• five exceptions and their handling

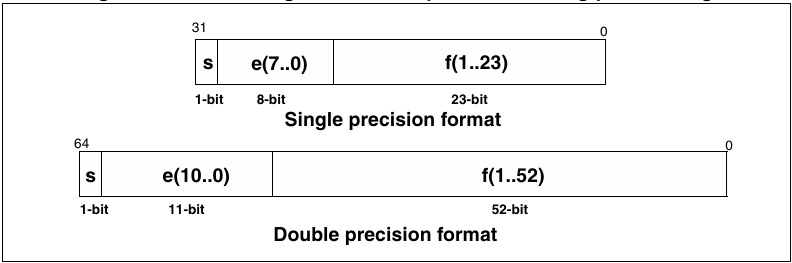
All values are composed of three fields:

• Sign: s
• Biased exponents:
  • sum of the exponents = e
  • constant value = bias
• Fraction (or mantissa): f The values can be coded on various lengths:
• 16-bit: half precision format
• 32-bit: single precision format
• 64-bit: double precision format

Normalized numbers

Normalized numbers are given by the formula below: 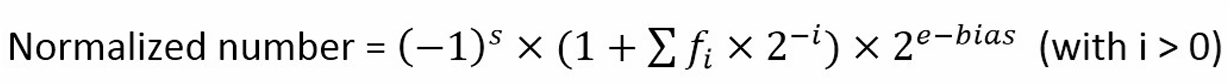The bias is a fixed value defined for each format (8-bit, 16-bit, 32-bit and 64-bit)

Denormalized

Denormalized (or subnormal) numbers are used when the value to represent is too small to be encoded as a normalized number. In this case, the exponent is set to zero, and the precision is slightly reduced to allow for gradual underflow.

This ensures smoother transitions around zero and allows representation of values closer to zero than what normalized numbers can express.

Format	Min Denormalized Value
Half	~5.96×10⁻⁸
Single	~1.4×10⁻⁴⁵
Double	~4.94×10⁻³²⁴

🔁 Example 1: Convert Decimal to IEEE 754 Single-Precision

Input: -7.0
We’ll convert -7.0 to IEEE 754 single-precision (32-bit) floating-point format.

Step 1: Sign bit

Since it’s negative → Sign = 1

Step 2: Convert to binary

7.0 in binary = 111.0 = 1.11 × 2² (normalized form)

Step 3: Exponent

• Bias for single precision = 127
• Exponent = 2 → 2 + 127 = 129
• 129 in binary = 10000001

Step 4: Mantissa (23 bits)

Keep the fraction part after the 1. (since 1. is implicit in normalized form)
1.11 → take .11 → 11000000000000000000000

✅ Final IEEE 754 Format

Sign	Exponent	Mantissa
1	10000001	11000000000000000000000

In Hex:

0b1_10000001_11000000000000000000000 = 0xC0E00000

---

🔁 Example 2: Convert IEEE 754 Hex to Decimal

Input: 0xC0E00000

Step 1: Binary Breakdown

0xC0E00000 →
11000000111000000000000000000000

• Sign: 1 → negative
• Exponent: 10000001 → 129
• Mantissa: 11000000000000000000000

Step 2: Compute Exponent

129 - 127 = 2

Step 3: Compute Mantissa

Add implicit 1. in front → 1.11
Binary 1.11 = 1 + 0.5 + 0.25 = 1.75

Step 4: Final Result

Value = -1.75 × 2² = -7.0

---

🧠 Summary Table

Decimal	IEEE 754 Binary	Hex
-7.0	1 10000001 11000000000000000000000	0xC0E00000

Special Values in IEEE 754

IEEE 754 defines several special cases in floating-point representation:

• Zero: Represented by all exponent and mantissa bits being 0. The sign bit determines +0 or -0.

• Infinity (±∞): Occurs when the exponent is all 1s and the mantissa is all 0s.

• NaN (Not-a-Number): Used to represent undefined or unrepresentable values such as 0/0 or sqrt(-1).

• Quiet NaN (QNaN): Propagates silently through most operations.

• Signaling NaN (SNaN): Triggers an exception when used.

Sign	Exponent	Fraction	Meaning
0	0	0	+0
1	0	0	-0
0	Max	0	+∞
1	Max	0	-∞
x	Max	≠0	NaN (Q/S)

Rounding Modes

IEEE 754 specifies 4 rounding modes, which affect how results are approximated when they can’t be represented exactly:

• Round to Nearest (default): Chooses the nearest representable value. If tie, rounds to even.

• Round Toward Zero: Truncates the result.

• Round Toward +∞: Rounds up.

• Round Toward −∞: Rounds down.

• Rounding mode can be selected via the FPU configuration registers such as FPSCR or FPDSCR.

Exception Handling

Floating-point operations can raise exceptions in five situations:

• Invalid Operation (e.g., sqrt(-1), 0/0)

• Division by Zero

• Overflow (result exceeds the maximum value)

• Underflow (result is too close to zero to be normalized)

• Inexact Result (result had to be rounded)

In STM32:

• Exceptions are handled via interrupts, not traps.

• Flags like IOC, DZC, OFC, UFC, IXC are set in FPSCR.

• You can monitor or clear these flags manually.

Using FPU in STM32 Projects

To benefit from the hardware FPU on STM32:

✅ Enable FPU in Compiler Settings
MDK-ARM (Keil): Enable -mfpu=fpv4-sp-d16 or fpv5-d16 based on your target.

GCC: Use -mfpu=fpv4-sp-d16 -mfloat-abi=hard for single-precision FPU.

⚙️ Use Native Float Instructions Use float or double in your C code. The compiler will generate optimized FPU instructions if -mfloat-abi=hard is set.

🧠 Avoid Mixing Soft/Hard FPU Mixing -mfloat-abi=soft and -mfloat-abi=hard across modules may lead to linking errors. Stick to one strategy.

💾 Context Saving